あらすじ
以前まで続けていた Julia コンパイラの内部構造についての記事について、一旦これまでの知見を使って簡略化した Julia のコンパイルプロセスを実装します。
そのほかの Juia コンパイラに関連する記事は
Julia と 型推論
まず最初に、(みんなが思い浮かべるものという意味で) 一般的な型推論と少し違うのもあるので、Julia における型推論の利用のされ方について少し書きます。
型推論 ?
とくに意識して記述せずとも、特定の式が実行時にとりうる値の型についていくらかの非自明な事実が常に成り立っていることはよくあります。
x = 1
x + 1 # <- 絶対 `Int`
のように書けば、
x + 1 の値は Int です。 リテラルがなくとも、
name = readline() # <- String
msg = "Hello, $(name)!" # <- String
では、
name も msg もつねに String になるでしょう。 さらに、
if x isa Number # <- `x` の値の型は `Number` 型の子か?
println("数字:", x)
elseif x isa AbstractString # <- `x` の値の型は `AbstractString` 型の子か?
println("文字列:", x)
end
という条件分岐を考えると、それぞれの条件分岐の中では
-
xはNumber(Int64,Int32,Float64などの親) -
xはAbstractString(String,LazyStringなどの親)
という事実が常に成り立ちます。
この記事では Julia の Docs にならい 、このような事実の導出─ 「あるコントロールフローにおいてある式が取りうる値の型情報を静的に導くこと」を 型推論 (Type Inference) と呼ぶことにします。
Julia の処理系の特徴の一つは、この意味での型推論を行なうことです。 そしてさらに特徴的な点は、得た情報をもっぱらパフォーマンス向上のために使うことです。
まずは型推論によってパフォーマンスを向上させることができる例を見てみます。
パフォーマンス向上例: ディスパッチの静的な解決
二つの整数を受け取って、その総和を計算する関数を考えます。
add(a::Int, b::Int) = a + b
これを、ユーザ定義型
MyInt の組にも使えるようにしてみます。 この MyInt は加算するとついでに 100倍されます。 [scitokyo]struct MyInt
v::Int
end
add(a::MyInt, b::MyInt) = MyInt((a.v + b.v) * 100)
つまり、
add という generic function (総称関数) があって、-
Intを普通に足すもの -
MyIntを100倍されて足すもの
という 2つのメソッドが存在することになります。
このとき、Julia の処理系は
a = MyInt(1)
b = MyInt(1)
add(a, b) # => MyInt(200)
のような関数呼び出しを行う際に、すべての引数の実行時の値の型に基づいて
add(a::MyInt, b::MyInt) = MyInt((a.v + b.v) * 100) という実装を選択して実行してくれます。(多重ディスパッチといいます)複数のマッチする実装があるときは、そのうちもっとも「特化したもの」が選ばれます。 例えば
f(x::Real, y::Real) = add_with_error_handle(x, y)
f(x::Int, y::Int) = x + y
という
f があったときは f(1, 2) という呼び出しは下のメソッドが呼び出されます。 (Real, Real) という型の組より (Int, Int) のほうが「特化している実装」だからです。多重ディスパッチを行うためには 引数
a , b の型が判明していないといけないわけですが、Julia の処理系は実装の選択を実行時に行うことでこれを常に可能にしています。しばしば混同される機能として、例えば C++ などにあるオーバーロードがありますが、オーバーロードは多重ディスパッチと異なり静的に実装を選択します。
また Python や Java の標準的な Class のように引数のうち一つを特別視して実装を選択 (シングルディスパッチ) せずに、全ての引数から実装を選択するのも多重ディスパッチの特徴です。
また Python や Java の標準的な Class のように引数のうち一つを特別視して実装を選択 (シングルディスパッチ) せずに、全ての引数から実装を選択するのも多重ディスパッチの特徴です。
さて、多重ディスパッチによる実装の選択は、ものすごくざっくり書けば、
function call_generic(fname, args)
argtypes = typeof.(args) # (1) 引数の値の型チェック
matched = lookup(methodtable, fname, argtypes) # (2) マッチするメソッドを検索
invoke(matched, args) # (3) 実行
end
のようなことをしているわけです。
しかし、これを実行時に行うと 毎回
typeof.(args) を呼び出し、メソッドテーブルに検索をかけるコストがかかります。ところがどっこい、型推論によって例えば 「引数は全て つねに
MyInt である」ことなどが導ける場合、この型チェックと検索をスキップして、直接特定のメソッド呼び出し (この場合は (a.v + b.v) * 100 ) にすることができます!これは型推論によってパフォーマンスを改善できる代表的な例です。
実際に Julia コンパイラがそのような最適化を行なっていることを確認してみましょう。
下のような二つの関数
f , g を考えます。julia> a = [1, 2, 3]
3-element Vector{Int64}:
1
2
3
julia> const b = [1, 2, 3]
3-element Vector{Int64}:
1
2
3
julia> function f(c)
d = c * a
return sum(d)
end
f (generic function with 1 method)
julia> function g(c)
d = c * b
return sum(d)
end
g (generic function with 1 method)
どちらも
c * [1, 2, 3] の総和を計算する関数ですが、 [1, 2, 3] の出どころが -
f: ただのグローバル変数 -
g:const宣言したグローバル変数
という違いがあります。実は、このことは型推論をする上で大きな差を生みます。
というのも、
const 宣言されていないグローバル変数は常に任意の型の値に書き換えれられる可能性があるので、Julia コンパイラはその型を Any と推論するからです。確認してみましょう。
Julia にはコンパイラが何を考えているのかを調べる手段がたくさん備わっており、例えば
@code_typed マクロを使うと型推論の結果やそれに基づく最適化を施した結果を見ることができます。まず
f(1) は以下のようになります。julia> @code_typed f(1)
# CodeInfo(
# 1 ─ %1 = Main.a::Any # <- Any と推論されている
# │ %2 = (c * %1)::Any # <- それとの積は `Any`
# │ %3 = Main.sum(%2)::Any # <- `sum` という generics 呼び出しのまま
# └── return %3
# ) => Any # <- `f(1)` 自体も `Any` と推論
計算過程の式は全て
Any と推論されていて、返り値も Any となっています。 さらに、 sum という generic function の呼び出しがそのまま残っていますね。一方
g(1) は (長いので出力をかなり省略しています。ぜひ手元で試してみてください)julia> @code_typed g(1)
# CodeInfo(
# 1 ── %1 = invoke Main.:*(c::Int64, Main.b::Vector{Int64})::Vector{Int64}
# ...
# 9 ┄─ %28 = Base.getfield(%1, :ref)::MemoryRef{Int64}
# │ %29 = Base.memoryrefnew(%28, 1, false)::MemoryRef{Int64}
# │ %30 = Base.memoryrefget(%29, :not_atomic, false)::Int64
# └─── goto #10
# 10 ─ goto #32
# 11 ─ %33 = Base.slt_int(%8, 16)::Bool
# └─── goto #31 if not %33
# ...
# 31 ─ %98 = invoke Base.mapreduce_impl(%4::typeof(identity), %5::typeof(Base.add_sum), %1::Vector{Int64}, 1::Int64, %8::Int64, 1024::Int64)::Int64
# └─── goto #32
# 32 ┄ %100 = φ (#3 => 0, #10 => %30, #30 => %72, #31 => %98)::Int64
# ...
# │ %118 = Base.not_int(%117)::Bool
# └─── goto #46 if not %118
# 45 ─ goto #2
# 46 ─ return %110
# ) => Int64
返り値は
Int64 と推論されていること、そして sum の呼び出しは消えて具体的な実装に置き換えられていることがわかります。さらによく見ると、 slt_int のような Int 向けの特化した関数が使われているのがわかると思います。実行速度を調べると
julia> @benchmark f(1)
BenchmarkTools.Trial: 10000 samples with 994 evaluations per sample.
Range (min … max): 30.978 ns … 2.146 μs ┊ GC (min … max): 0.00% … 97.90%
Time (median): 33.284 ns ┊ GC (median): 0.00%
Time (mean ± σ): 36.100 ns ± 46.637 ns ┊ GC (mean ± σ): 7.44% ± 6.10%
▁▂▁▁▇▇▅▃▂▅██▄▃▅▃▂▁ ▁▃▃▁ ▂
███████████████████████▇▇▇▇▆▇▇▆▆▅▅▆▅▆▆▂▅▅▅▅▆▇▄▅▆▅▅▅▄▅▅▄▅▅▅▆ █
31 ns Histogram: log(frequency) by time 44 ns <
Memory estimate: 80 bytes, allocs estimate: 2.
julia> @benchmark g(1)
BenchmarkTools.Trial: 10000 samples with 998 evaluations per sample.
Range (min … max): 15.281 ns … 1.825 μs ┊ GC (min … max): 0.00% … 98.33%
Time (median): 15.949 ns ┊ GC (median): 0.00%
Time (mean ± σ): 18.962 ns ± 52.555 ns ┊ GC (mean ± σ): 13.34% ± 4.96%
▄▆▆██▇▆▅▄▄▂▃▃▃▂▂▂▁ ▁ ▁▁▂▁▁ ▁ ▁▂▁▁ ▂
███████████████████████████████▇██████▇▆▇▇▆▅▅▆▅▆▆▆▅▅▆▅▆▃▆▇▇ █
15.3 ns Histogram: log(frequency) by time 22 ns <
Memory estimate: 80 bytes, allocs estimate: 2.
と、
g(1) の方が 2 倍近く高速です!こうして Julia 言語は型推論に基づく最適化で良好なパフォーマンスを得ていることがわかりました。
このような例を出すと「Julia ではパフォーマンスを出すにはコンパイラの気持ちを理解しなければいけないのか」となるかも知れませんが、Julia コンパイラは大変賢く、パフォーマンスのために気をつける必要があることは (少なくとも同じような「簡潔だけど高速」という売り込みの言語に比べれば) かなり少ないというのが私の印象です。
そのほかの特徴
Julia の型推論プロセスが持つ特徴としては、以下のようなものがあります。
1 推論は できる限り 行われる
Julia の処理系は推論精度 (による実行時間の短縮) とコンパイル時間とのトレードオフに気を使って実装されています。
インタラクティブに行いたい科学技術計算ではコンパイル時間がいたずらに長くなるような処理系の体験はとても悪くなるからです。
理論的に達成できる限界まで精度よく推論できなくても実行自体はできるので、実は導出可能であってもコンパイル時間の短縮のため推論を行わないこともあります。
2 推論のエントリポイントは関数呼び出し
Julia の関数はあたらしい引数の型の組で呼び出されたまさにそのときにコンパイルされ、実行されます。 そのため、Julia の型推論プロセスは、渡された具体的な値の型から出発します。
3 推論は inter-procedural に行われる
Julia の型推論は関数境界を跨いで行われます。つまり、ビルトイン関数とは限らない (= 返り値の型が明らかでない)
g の呼び出しを含む f をコンパイルする際、 g に対する推論も行われます。まとめると、以下のようになります。
Julia の型推論プロセスのまとめ
Julia の型推論プロセスは
プロセス。
Julia の型推論プロセスは
- 関数の実際の実行を始めようとする まさにそのときに
- その引数の 値の型 から
- ある箇所での変数の型の情報を
- 関数境界を跨いで 再帰的に
- できる限り 推論する こと
- (でパフォーマンスを向上させる)
プロセス。
また、得られる型情報の利用のされ方も一般的な静的型付け言語とはかなり異なります。
Julia は JIT コンパイル[jitcompile] で動作する動的型付けの言語です。コンパイル時に型検査は行われず、例えばメソッドが存在しないことがコンパイル時にわかってもコンパイルエラーなどとはせず、実行時例外になります。
myadd(a::Int, b::Int) = a + b
function main()
println("Start to execute main~~")
myadd(0.2, 0.3) # <- `myadd` は (Float64, Float64) に対しては実装がない
end
main()
# ↓
# ↓
# julia> include("no_method.jl")
# Start to execute main~~
# ERROR: LoadError: MethodError: no method matching myadd(::Float64, ::Float64)
# The function `myadd` exists, but no method is defined for this combination of argument types.
#
# Closest candidates are:
# myadd(::Int64, ::Int64)
# @ Main ~/Desktop/mu/no_method.jl:1
その意味で、こと Julia コンパイラ本体においては型推論はほとんどパフォーマンスのためのいち情報に過ぎないわけですが、本体にないだけで Julia の型推論を使って静的にエラーチェックをしたり、rutime-dispatch などを検知するパッケージなどもあります。
ここでは JET.jl を紹介します。
https://github.com/aviatesk/JET.jl
julia> using JET
julia> myadd(a::Int, b::Int) = a + b
myadd (generic function with 1 method)
julia> function main()
println("Start to execute main~~")
myadd(0.2, 0.3)
end
main (generic function with 1 method)
julia> @report_call main()
═════ 1 possible error found ═════ # <- no method を発見
┌ main() @ Main ./REPL[3]:3
│ no matching method found `myadd(::Float64, ::Float64)`: myadd(0.2, 0.3)
└────────────────────
JET.jl は、Julia コンパイラの型推論プロセスを利用して、上のように
main の呼び出しで (Float64, Float64) に対する myadd の実装があるかを静的に検査してくれます。また、このようなツールの組み込みはまだ発展途上ですというのが正直な答えになってしまうものの、Language Server も一応あります。
https://github.com/julia-vscode/LanguageServer.jl
Julia の型システムそのものについての詳しい解説は (30 記事くらいになってしまうので) ここでは深くは触れません。
Julia の型推論までのプロセス
さて、ここからはこの型推論プロセスを作っていきます。
まずは実装を始める前に、型推論プロセスの入出力を明確にしておきましょう。

まず、Julia の処理系はソースコードをパースして (surface-) AST を作ります。
しかし、AST はそのままだと最適化が実装しにくいので、Julia の型推論は AST を最適化しやすいよう変形した IR に対して行われます。(この処理は lowering と呼ばれます)
実際にはさまざまなコンパイラへのヒントなども含みますが、使われる IR はざっくり言ってしまえば
- マクロが全て展開されて
- 全ての糖衣構文 (for, 三項演算子など) が解体されて
- GOTO を使った直列の命令列への書き直し (linearize) が行われた
形式です。
Meta.lower によって実際に AST から IR に変換した結果を見ることができるのですが、julia> lowered_ir = Meta.lower(Main,
quote
for i in 1:10
println(i)
end
end
)
# :($(Expr(:thunk, CodeInfo(
# @ REPL[23]:3 within `top-level scope`
# 1 ─ %1 = :
# │ %2 = (%1)(1, 10)
# │ #s2 = Base.iterate(%2)
# │ %4 = #s2
# │ %5 = %4 === nothing
# │ %6 = Base.not_int(%5)
# └── goto #4 if not %6 # <- goto が生えてる
# 2 ┄ %8 = #s2
# │ i = Core.getfield(%8, 1)
# │ %10 = Core.getfield(%8, 2)
# │ @ REPL[23]:4 within `top-level scope`
# │ %11 = i
# │ println(%11)
# │ @ REPL[23]:5 within `top-level scope`
# │ #s2 = Base.iterate(%2, %10)
# │ %14 = #s2
# │ %15 = %14 === nothing
# │ %16 = Base.not_int(%15)
# └── goto #4 if not %16 # <- goto が生えてる
# 3 ─ goto #2 # <- goto が生えてる
# 4 ┄ return nothing
# ))))
なんだかごちゃごちゃしているように見えるかもしれませんが、for 文が解体されて条件付き goto を使った直列の命令列への書き換えがされていることがわかります。
このような IR も Julia 自体での表現 (
CodeInfo 型) を持つので、触って遊ぶことができます。julia> lowered_ir.args[1].code[1:10]
10-element Vector{Any}:
:(Core.get_binding_type(Main, :i))
:(_1 = 0)
:(_1)
:(%3 isa %1)
:(goto %7 if not %4)
:(goto %9)
:(_1)
:(_1 = Base.convert(%1, %7))
:(_1)
:(i = %9)
一方で lowering の処理それ自体は現在は C や Scheme で実装されているのですが、最近は Julia によって書き直すプロジェクトが進んでおり、いずれは Julia で完結するかもしれません。(パーサもかつては Scheme 製でしたが今は Julia製のものが動いています。https://github.com/JuliaLang/JuliaSyntax.jl)
https://github.com/c42f/JuliaLowering.jl
この lowerd IR を受け取り、型情報を付加したものを出力するのが目標です。

Julia の型推論アルゴリズム ─ 抽象解釈
Julia の型推論は、抽象解釈という枠組みのもと構築されています。
最初にも書きましたが、これを正確に説明することにすると大変なボリュームになってしまうので、詳しい話は
抽象解釈は、簡単に言えば
プログラムの具体的な値を少し抽象化して「評価」する枠組み
のことです。例えば
- 現れるのはすべて自然数
- 演算は掛け算だけ
という言語で、
if cond
x = 1
else
x = 2
end
y = 2 * x
y
というプログラムがあったとします。 このとき、ある変数がある命令の実行直前,直後に 偶数であるか? 奇数であるか?というのを解析することを考えてみます。
抽象解釈は、元のプログラムの変数を例えば 「偶数か奇数」「偶数」「奇数」「未定義」というような抽象状態に割り当てることによって行います。
つまり上のプログラムを
x? <= 未定義
y? <= 未定義
if cond
x = 奇数
else
x = 偶数
end
x? <= (奇数 または 偶数)
y = 偶数 * (奇数 または 偶数)
y? <= 偶数
というように評価するわけです。 (ここで、「実行」という言葉を使わなかったのは、もとのプログラムと同じ順序で制御フローを辿って評価するとは限らないからです)
そして、この評価は
- リテラルの代入は (元のプログラムの) 右辺の値の偶奇が入る
- 掛け算の代入は (奇数) (奇数) は奇数, (奇数) (偶数) は偶数, ...
という抽象化したもとでの意味関数を定めることによってできます。
さらに、抽象状態の間には取りうる値の包含関係、つまり「具体度」「情報量」と捉えられる順序が定められます。
今回は 「未定義」 \( \leq \) 「偶数」 \( = \) 「奇数」 \( \leq \) 「偶数または奇数」 という感じでしょうか。

このもとで、なるべく具体的なものを求めましょう. という形に定式化することで、できる範囲で正確な静的解析を行うようなアルゴリズムを考えることができます。
さて、この 偶数 or 奇数? というのを型っぽいものに置き換えれば型の静的な解析ができそうなのは何となく理解できるかと思います。
なので問題は
- このような抽象的な評価はどのくらいまでなら詳しくできるのか ?
- 型レベルに抽象化した評価、というものは出来るものに含まれるのか ?
になります。
(例えば具体的な値と完全に対応させればそれはただの具体的な実行ですが、これは当然停止しないこともあります)
そこでこのくらいなら解けますよ. というのが考えられています。
先ほども書いたようにここでその話を展開すると同人誌になってしまうので、気になる方は上のリンクを踏んでもらえればと思います。
ここでは今回利用する結果だけを簡単に述べます。
抽象解釈の枠組みで、「ある命令の実行前後でプログラムの抽象状態のうちなるべく具体的なものを求める」という問題である「データフロー解析問題」を解くことができます。
データフロー解析問題に対しては、抽象状態とその順序, そして意味関数が
- 意味関数が単調
- 抽象状態と順序関係が無限上昇鎖を持たない束をなす
という条件を満たすときに停止する求解アルゴリズムが知られています。
一つ目の条件は、順序が具体度を表すことにすると
「より具体的な状況で関数を実行した結果は、より具体的になる」
と表現できるわけで、これは自然な条件です。
二つ目の条件についてここで説明するのはやや大変です。投げやりで申し訳ないですが、やはり先ほどのリンクを見てください。
今回もこれを使って型推論を行います。
作るもの 〜 理論編 〜
では、実際に Julia の処理系を模倣した簡易的な処理系を作っていきます。 (mu という名前をつけました。)
実装はすべて
https://github.com/abap34/mu
に置いておきます。(良かったら star つけてください)
今回作る言語は多重ディスパッチをサポートします。つまり、
function f(x::Int, y::Int){
return complex_function(x, y)
}
function f(x::Real, y::Real){
_check_calcuable(x, y)
return complex_function(x, y)
}
function main(){
f(1, 2) # => complex_function(1, 2)
f(1.0, 2.0) # => _check_calcuable(1.0, 2.0); complex_function(1.0, 2.0)
}
のような結果を得ることができます。
さらに、このディスパッチを静的に解決ができる場合は解決することにします。 つまり、
f(x, y) という呼び出しにおいて x , y は Int だ、などという事実が導けた場合にはディスパッチを実行時にはノーコストで行えるようにします。 (つまりチェックがノーコストでスキップされます)型
簡単のために、ユーザ定義型は作れないことにして、この言語に現れる型は以下で固定されているとします。
-
Any -
Bottom -
Number -
Real -
Int -
Float -
Bool -
AbstractString -
String -
Union{T, U ...} -
Tuple{T, U ...} -
AbstractArray -
Array{T, n}
まずは一部の見慣れない型の説明を含めて、この言語がとる型システムについて少し書きます。
また、このシステムは Julia の型システムを模倣したものになっています。
型の階層構造
この言語の型の集合は以下のような親子関係で半順序集合をなします。
型
B が A の 親であることを A <: B とかくことにして、 親子関係
A である値の集合が B である値の集合の部分集合であるとき、またそのときに限り A <: B この考え方にそって、今回登場する型に以下のようなグラフで表されされるような親子関係を定めます。
このグラフに現れる型の組については、
A と B が同じか、このグラフの Any から Bottom への経路であって、 B が A よりも先に出てくるものがあるとき、またそのときに限り B は A の親です。
例えば
Int <: Real , Int <: Int , Float <: Number です。具象型と抽象型
ここで、上のグラフで、頂点がオレンジと水色で塗り分けられていましたが、
これは、今回の言語の型システムにおける 具象型 (Concreate Type) と 抽象型 (Abstract Type) を表しています。
具象型はインスタンスが作れる型のことです。
つまり、
x の値の型を取得する関数 typeof(x) のような関数があったとき、これの返り値は必ず具象型になります。抽象型である Any , Number などが返ることは決してありません。今回の場合
Int , Float , Bool , String などが具象型にあたります。抽象型は具象型をまとめて構造化して、多重ディスパッチの制御をしやすくすることがその役割です。
Array{T, n} 型
Array{T, n} 型の説明をしましょう。これは、全ての要素の型が全て
T の子である n 次元配列です。[arrayattent]{T, n} は型パラメータと呼ばれるもので、例えば Array{String, 1} として文字列からなる 1次元配列を、 Array{Real, 2} で実数 (今回は Int または Float ) からなる 2次元配列などを表現できます。型パラメータを導入したときに考える必要があるのが次のような問いです。
Array{Real, 1} は Array{Int, 1} の親か?今回の型システムは、
Array について以下のような規則を採用することにします。 不変性 (Invariance)
Array{T} は B \( \neq \) C なる 任意のパラメータ B , C について Array{B} と Array{C} は親子関係でない。つまり、
Array{Real, 1} は Array{Int, 1} の親ではないことにします。 このような性質─
- 型パラメータ
Tを持つ型A{T}が 任意の相異なる型パラメータS,Tに対して (たとえS <: Tであっても)A{S} <: A{T}でない
のことを 不変性 (Invariance) といいます。
不変性を採用することが仕様として絶対の正解かというと全然そんなことはなく、 そもそも Julia の型システムにおいても例外が存在しますし(後述します)、色々な言語でいろいろなシステムが採用されています。逆に
B <: C ならば A{B} <: A{C} という性質を 共変性 (Covariance) といいます。これらの説明も長くなってしまうので気になるかたはこれらのワードで検索してください。
とにかく、こっちを採用したことによって先ほどの親子関係がなす階層構造はこんな感じになります。
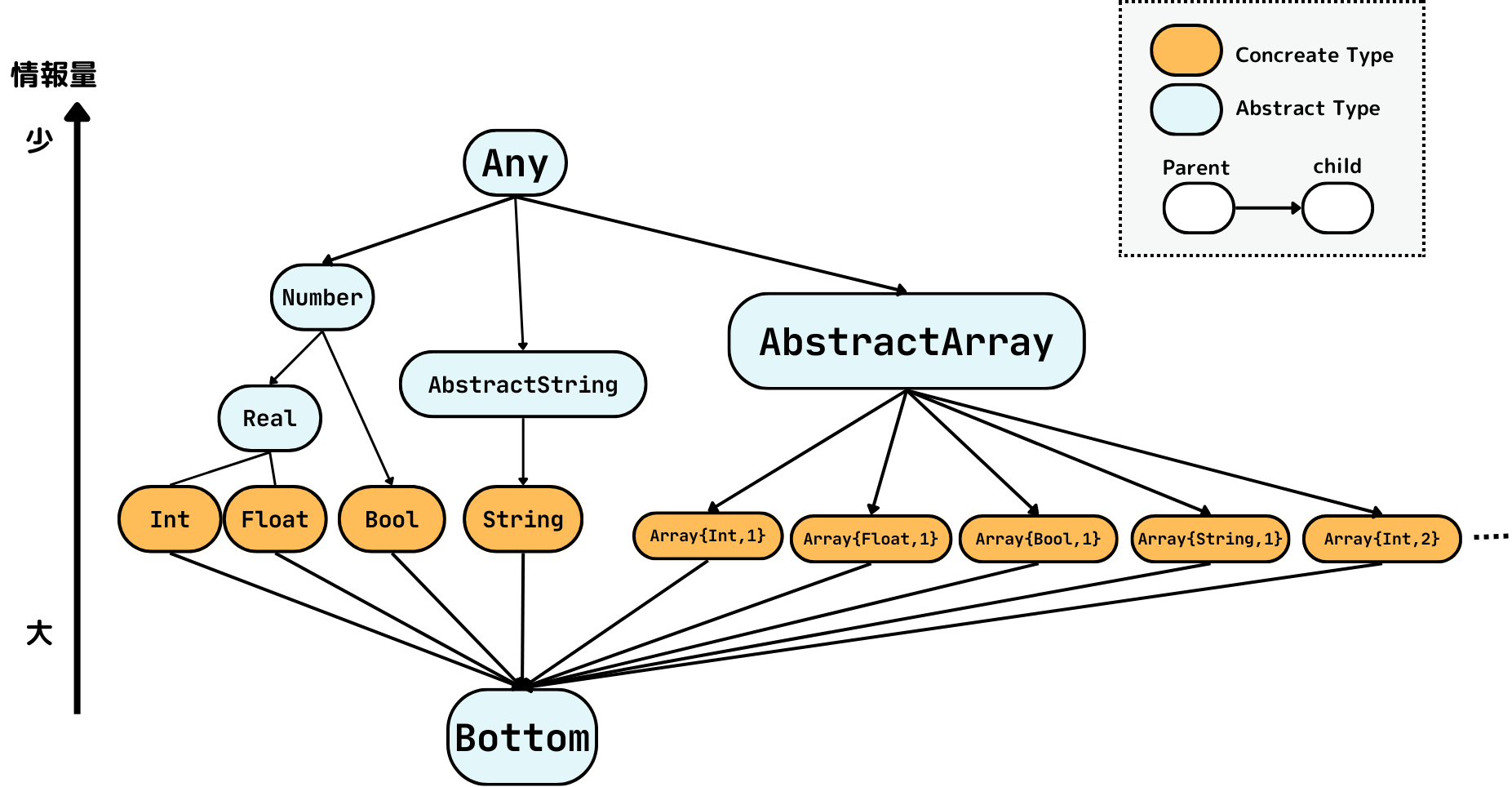
型パラメータとして
n が追加されたことで、型の数が有限でなくなりました。 Any 型
Any 型は簡単にいうと任意の値を表す抽象型です。 取りうる値がこの言語に存在するすべての値であることを表します。今回はこれが親子関係における最大元、つまり任意の型
T に対して T <: Any な型になります。 Bottom 型
となると、逆に取りうる値が存在しないことを表す型が最小元となります。
今回はこれを
Bottom という名前にすることにします。つまり 任意の型
T に対して Bottom <: T です。 Tuple 型
Tuple は値の組を表す型で、型パラメータとして型の組を取ります。
例えば
(1, 2.0, 3) は Tuple{Int, Float, Int} の値です。ここで注意点として、
Tuple 型は共変性を持つことにします。 例えば Tuple{Int, Float, Int} <: Tuple{Int, Real, Real} です。というのも、
Tuple 型 がシグネチャを表現するために用いられるからです。多重ディスパッチの説明で書いたように、メソッドを選択する際には引数の型のうちどれがもっとも特化されているかを調べる必要があります。この比較を成り立たせるには共変性を持たせるのが自然です。
Tuple 型も型パラメータとして任意個の型を取りますから、これを導入するとやはり型の集合が無限個になってしまいます。 Union 型
Union 型は、型パラメータとして非空の [bottom] 型の集合を取ります。これは名前の通り和集合の表現に近く、
S <: Union{S, T, U} , T <: Union{S, T, U} , U <: Union{S, T, U} です。Union 型を含む親子関係は Julia の仕様に沿って以下のように定めます。[juliasubtyping]Union 型 U (型パラメータ T ) と 型 S の親子関係 T の全ての要素が S の子であるとき、またそのときに限り U <: S ある T の要素が存在して S の親であるとき、またそのときに限り S <: U Tuple型も含む親子関係
Union 型の親子関係は Tuple も絡むとよりややこしくなります。というのも、同じ集合を表す複数の表現が存在するからです。例えば
Tuple{Int, Union{Int, Float}} は Union{Tuple{Int, Int}, Tuple{Int, Float}} と等価です。簡単な実装の仕方としては、適当な標準形に変換してしまって比較するという方法があります。 例えば
Union はトップレベルにのみ存在するように変換するのは容易です。この方法は実装は容易ですが型パラメータのネストの深さに対して指数時間かかります。 なので Julia の処理系ではより高速な方法が用いられています。[fastsubtyping]
このように親子関係の判定は実は少しややこしく、進んだ面白い結果として、少し前までは Julia の親子関係の判定は決定不能であったというものがあります。[juliasubtypingdecide]
さて、こと型推論のことを考えると、if文の分岐でそれぞれ
Int , Float が返るようなケースでは Union{Int, Float} のように表現できそうですから、これを導入することによって強い表現力が得られそうな感じがします。function f(x)
if x > 0
return 1
else
return 1.0
end
end # => Union{Int, Float64}
しかし、強いものの計算が大変なのは世の常です。
Union 型は強力ですが型システムの取り扱いをとてもややこしくします。ここからはそのことを見ていきます。
束としての性質 ─ 有限性条件の反例
今回考える (型の集合, 親子関係) は実は束になっています。
では型推論はデータフロー解析問題に落としこめばスッと解けるでしょうか?
実はこのままだとうまくいきません。 データフロー解析問題の反復解法はその停止性のために
- 意味関数の単調性
- 抽象状態の束の高さの有限性
を要求していました。しかし、今回は以下のような無限長の上昇鎖が構成できてしまいます。
Union{Vector{Int, 1}}
<: Union{Array{Int, 1}, Array{Int, 2}}
<: Union{Array{Int, 1}, Array{Int, 2}, Array{Int, 3}}
<: Union{Array{Int, 1}, Array{Int, 2}, Array{Int, 3}, Array{Int, 4}}
...
型集合が無限にあること、
Union 型が存在することによってこのような問題が発生してしまったわけです。なので、単純に前回のアルゴリズムを適用するだけでは収束性が保証されません。
プログラムの具体的な実行が停止する保証は当然しなくていいわけですが、 コンパイルプロセスは、それがたとえ不正なプログラムであったとしても必ず停止させなければいけません。
そこで Widening と呼ばれる抽象解釈で一般的なテクニックを使うことでその停止性を復活 (?) させます。
一旦、いろいろ忘れて Widening についてみていくことにします。
Widening
Widening は、(今の状態, 更新したい状態) から次の状態を出力する \( \nabla \) に望ましい性質を持たせることで無限長の鎖を有限回で登り切れるようにスキップするテクニックです。
まずは定義と例を紹介します。
Widening Operator
\( (P, \leq) \) が半順序集合であるとする。
\( \nabla: P \times P \rightarrow P \) が次のような性質を満たすとき、 \( \nabla \) が (pair-) Widening Operator である という. [setwidening]
性質1 (被覆性)
任意の \( x, y \in P \) で \( x \leq x \nabla y \) かつ \( y \leq x \nabla y \)
性質2 (停止性)
鎖 \( x_0 \leq x_1 \leq x_2 \leq \cdots \) に対して、
\( y_0 = x_0, \\ y_{i+1} = y_i \nabla x_{i+1} \) と定める。このとき \( \\{ y_i \\}_{i \in \mathbb{N}} \) は次の性質を満たす。
[性質] ある \( k \) が存在して \( y_k = y_{k+1} = y_{k+2} = \cdots \)
具体例
\( P \) を、すべての整数区間の集合と最小元のための特別な要素を加えた集合、つまり
\( P = \\{ \bot \\} \cup \\{ [l, u] \mid l \in \mathbb{Z} \cup \\{ -\infty \\}, u \in \mathbb{Z} \cup \\{ \infty \\}, l < u \\} \)
として、区間の包含関係で \( \leq \) を定義します。 (ここで \( \bot \) は任意の区間 \( x \) について \( \bot \subseteq x \) なるとします)
そして、次のように \( \nabla \) を定めます.
\[
\begin{array}{ll}
\bot \nabla x = & x \\
x \nabla \bot = & x \\
{[l_0, u_0] \nabla [l_1, u_1] =} & \left[
\begin{array}{l}
\text{if } l_0 > l_1 \text{ then } -\infty \text{ else } l_0, \\
\text{if } u_0 < u_1 \text{ then } +\infty \text{ else } u_0
\end{array}
\right]
\end{array}
\]
このとき \( \nabla \) は Widening Operator です。
被覆性は明らかに成り立ちます。
停止性も左端・右端だけが拡大するケースと両方が拡大するケースをそれぞれ考えると、したがうのが簡単にわかります。

Widening の役割
更新時に Widening Operator を挟むことで無限に状態が更新されることがなくなるので ( \( \because \) 停止性)、一般の束に対して収束するデータフロー方程式の反復解法が作れます。
さらに、Widening には
- 近似精度の調節役
- 収束を早めるヒューリスティック
の役割を持たせることができます。
上の例ではすぐに諦めて区間を最大まで拡大したわけですが、例えば
- 幅 \( k \) まではそのまま持つ.
- 幅 \( k \) を超えたら \( [- \infty, + \infty] \) にする
ように \( \nabla \) を定義すれば、 \( k \) を調節することで望ましい程度に近似精度を調節することができます。
他にも、たとえ高さが有限であっても非常に高い束は解析が実用的でないことがあります。 (求解アルゴリズムの最悪計算量は束の高さに比例します)
そのようなときに適切に「スキップ」してくれる Widening Operator を導入することで、高速に収束させることができます。
さて、今回実装する型推論においても、Widening によって型推論の収束性を保証します。 どのような Widening を用いるかは実装のセクションで検討することにしましょう。
Widening を導入したデータフロー方程式の反復解法
前回の記事に載せたプログラムを再掲します。
(実は自明な効率化があり、それをすることで実際 Julia で使われているアルゴリズムと一致するのですが、それを書く時間がないのでここでは引き続きこれを使います。気になる方は
function abstract_interpret(I::Program, abstract_semantics::Function, a₀::AbstractState)::Vector{AbstractState}
n = length(I)
inputs = [copy(a₀) for _ in 1:n]
outputs = [copy(a₀) for _ in 1:n]
pred = build_pred(I)
while true
change = false
for i in 1:n
current_input = inputs[i]
current_output = outputs[i]
new_input = reduce(⊓, outputs[j] for j in pred[i]; init=copy(a₀))
new_output = abstract_semantics(I[i])(new_input)
inputs[i] = new_input
outputs[i] = new_output
if (current_input != new_input) || (current_output != new_output)
change = true
end
end
if !change
break
end
end
return [inputs; outputs[end]]
end
導入は簡単で、
outputs[i] の更新をするときに Widening Operator ∇ を挟めば良いです。停止性と元のアルゴリズムの証明と照らし合わせれば、このアルゴリズムの停止性がわかります。-function abstract_interpret(I::Program, abstract_semantics::Function, a₀::AbstractState)::Vector{AbstractState}
+function abstract_interpret(I::Program, abstract_semantics::Function, a₀::AbstractState, ∇::Function)::Vector{AbstractState}
n = length(I)
inputs = [copy(a₀) for _ in 1:n]
outputs = [copy(a₀) for _ in 1:n]
@@ -99,7 +99,7 @@ function abstract_interpret(I::Program, abstract_semantics::Function, a₀::Abst
new_output = abstract_semantics(I[i])(new_input)
inputs[i] = new_input
- outputs[i] = new_output
+ outputs[i] = ∇(new_output, current_output)
if (current_input != new_input) || (current_output != new_output)
change = true
Widening の被覆性は、順序関係 \( \leq \) でいうとより大きい方に結果を持っていくことを要求しています。
抽象解釈の枠組みにおいては、これはより情報量が少ない側に情報をまとめることに相当します。これによって Widening を導入してもその見積もりが危険になる (導けないはずの事実が導かれる) ことはありません。
まとめると、Widening は以下のようなものです。
Widening
Widening は
- 解析の安全のための 被覆性
- 解析の停止のための 停止性
を満たした Widening Operator \( \nabla \) を状態更新の際に適用することで、状態更新を安全な側へ「スキップ」して有限時間でデータフロー解析問題を近似的に解くためのテクニック。
実装
それでは実際にこの世の全てを実装していこうと思います。
パース
これに関してはあまり今回の記事で本質パートでないので、少し軽めに説明します。
今回は PEG を使って構文を定義しました。お好きな方法でパーサを定義してもらえればと思います。 面倒であれば S式や json を入力にしてしまうという手もあります。
パーサのディレクトリ: https://github.com/abap34/mu/tree/main/src/parse
AST は Julia の構造を参考に、ノード自体の情報と子ノードを Vector で持つ形式にします。
@enum ExprHead begin
GCALL # Generic function call
BCALL # Builtin function call
ASSIGN # Assignment
IFELSE # If-else statement
IF # If statement
WHILE # While statement
PROGRAM # Special type to represent the whole program
BLOCK # Block to group multiple expressions
FUNCTION # For function definition
FORMALARGS # | Formal arguments for function definition
TYPEDIDENT # | Typed identifier. e.g. `a::Array{Int, 2}`
TYPE # | Type. e.g. `Array{Int, 2}`
RETURN # | Return statement
GOTO # Goto label without condition |
GOTOIFNOT # Goto label if condition is false | ==> These are for IR.
LABEL # Label for goto | Result of `parse` function will not have these.
end
struct Expr <: AbstractSyntaxNode
head::ExprHead
args::Vector{Any} # It is not avoidable to use `Any` here.
end
例えば
function main(){
x = [1, 2, 3]
n = 100
i = 0
while (i < n){
x = expanddims(x)
i = i + 1
}
return x
}
というコードをパースすると、
julia> mu.MuCore.parse(TESTCASE6) |> dump
# mu.MuCore.MuAST.Expr
# head: mu.MuCore.MuAST.ExprHead mu.MuCore.MuAST.PROGRAM
# args: Array{Any}((1,))
# 1: mu.MuCore.MuAST.Expr
# head: mu.MuCore.MuAST.ExprHead mu.MuCore.MuAST.FUNCTION
# args: Array{Any}((3,))
# ... 長いので省略 ...
# 2: Int64 0
# 4: mu.MuCore.MuAST.Expr
# head: mu.MuCore.MuAST.ExprHead mu.MuCore.MuAST.WHILE
# args: Array{Any}((2,))
# 1: mu.MuCore.MuAST.Expr
# 2: mu.MuCore.MuAST.Expr
# 5: mu.MuCore.MuAST.Expr
# head: mu.MuCore.MuAST.ExprHead mu.MuCore.MuAST.RETURN
# args: Array{Any}((1,))
# 1: mu.MuCore.MuAST.Ident
という AST が構築されます。S式っぽい見やすい printing を頑張って書くと
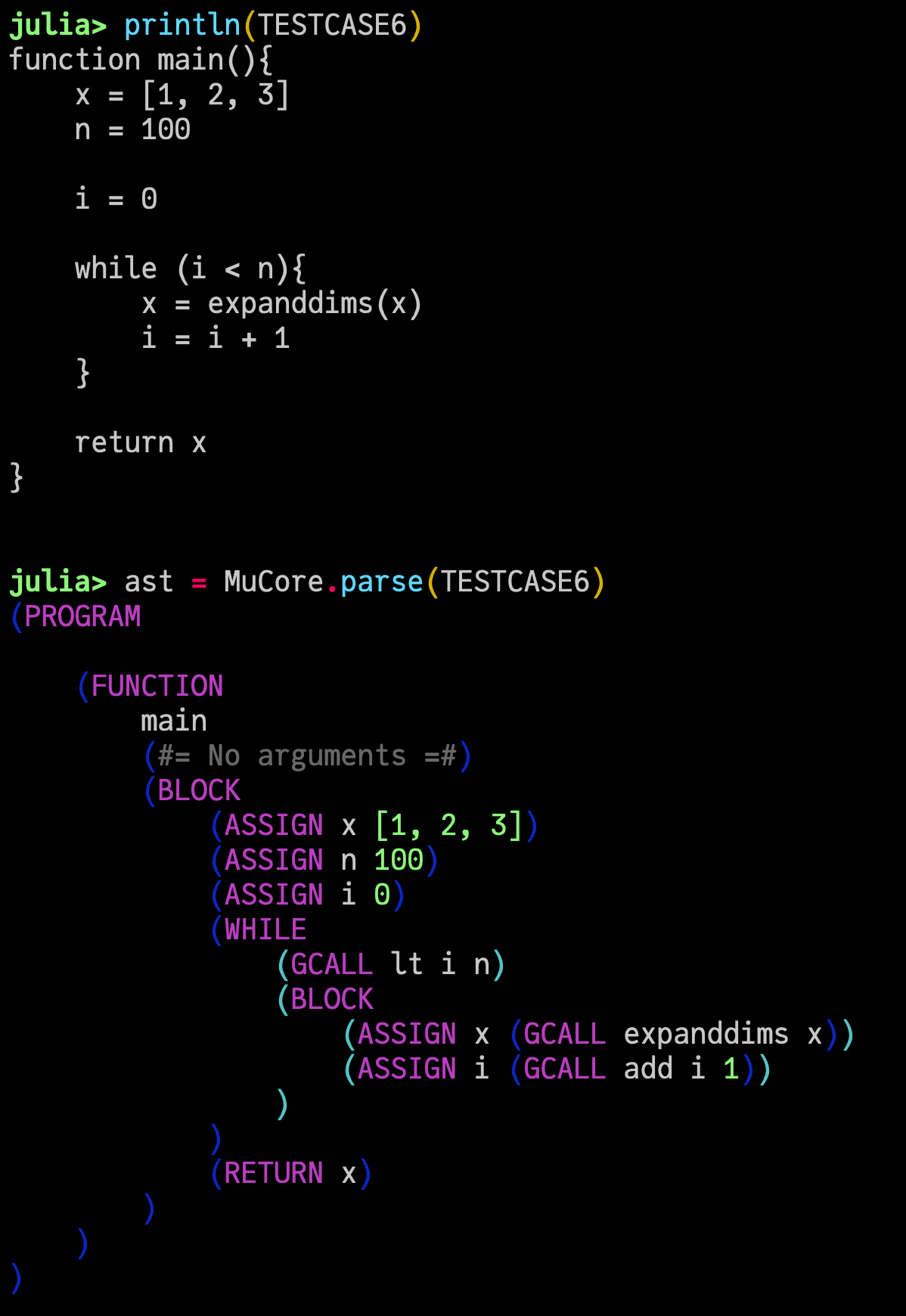
という感じです。
lowering
IR の表現
さて、lowering です。
これは
Expr を受け取って直列の命令列に変換するわけですが、今回の処理系では関数単位でこのような処理が行われます。まず、命令は
@enum InstrType begin
ASSIGN # Assignment
GOTO # Goto label without condition
GOTOIFNOT # Goto label if condition is false.
LABEL # Label for goto
RETURN # Return statement
end
struct Instr
instrtype::InstrType
expr::MuAST.Expr
end
と定義されて、IR はこれの列 (にいくらかの情報を持たせたもの) として定義します。
# Representation of program after lowering.
struct CodeInfo
instrs::Vector{Instr}
typed::Bool
varnames::Vector{MuAST.Ident}
vartypes::Vector{Union{DataType,Nothing}}
function CodeInfo()
return new(Instr[], false, MuAST.Ident[], Union{DataType,Nothing}[])
end
end
この上で、関数全体の lowering された後の表現を保持する
MethodInfo を定義します。関数名, 引数 (型アノテーションの情報も含みます), そして中身の IR を保持します。
# Information of each **method**.
struct MethodInfo
id::Int # id of the method (unique)
name::MuAST.Ident # Name of the method (not unique)
argname::Vector{MuAST.Ident} # Argument names (e.g. [`a`, `b`, `c`])
signature::MuTypes.Signature # Signature of the method. All elements must be MuTypes.
ci::CodeInfo # IR of the method
end
lowering の実装
それでは、上に示した表現への変換を実装します。
とはいえ、行うことは本当に場合わけを頑張ることのみです。
例えば、while 文の lowering の処理を見てみましょう。(https://github.com/abap34/mu/blob/33cedc918a83b4fd6ce8b8bc43f1e50236c5075a/src/lowering/lowering.jl#L157)
...
elseif expr.head == MuAST.WHILE
# while (cond)
# body
#
# ↓
# label cond_label
# goto end_label if not cond
# body
# goto cond_label
# label end_label
cond, body = expr.args
cond_label_id = label_gen()
end_label_id = label_gen()
pushlabel!(ir, cond_label_id)
pushgotoifnot!(ir, end_label_id, cond)
append!(ir, _lowering(body))
pushgoto!(ir, cond_label_id)
pushlabel!(ir, end_label_id)
else
...
コメントにもあるように、
while (cond) {
body
}
は
label cond_label
goto end_label if not cond
body
goto cond_label
label end_label
と変換することができます。なので、ラベルの id を生成して、上と一致するように順番に命令を追加していけば良いです。
注意が必要なものとしては、関数呼び出しの中で関数呼び出しが含まれるケースがあります。
y = 3 * x + 4
を考えてみます。これは、
julia> mu.MuCore.parse("y = 3 * x + 4")
(PROGRAM
(ASSIGN y (GCALL add (GCALL mul 3 x) 4))
)
という AST にパースされますが、中間変数
%1 を導入して%1 = (CALL mul 3 x)
y = (CALL add %1 4)
と lowering することにします。右辺が単一の関数呼び出ししかしないことにすると後の実装がしやすくなるからです。
なので、関数呼び出しに対しては
- 引数をチェック→ もし式なら新たに変数名 (e.g.
%1) を生成して、その式を lowering してその結果を生成した変数名に代入→ 定数, 変数ならそのまま
というのを再帰的に行うことで右辺を単一の変数呼び出しにします。

先ほどの関数の lowering 結果は以下のようになります。
julia> mu.MuCore.lowering(ast)
# 1-element Vector{mu.MuCore.MuIR.MethodInstance}:
# function main()
#
# | idx | instrtype | instr
# | --- | ---------- | ----------------------------------------
# | 1 | ASSIGN | x = [1, 2, 3]
# | 2 | ASSIGN | n = 100
# | 3 | ASSIGN | i = 0
# | 4 | LABEL | LABEL #29
# | 5 | ASSIGN | %32 = (GCALL lt i n)
# | 6 | GOTOIFNOT | GOTO #30 IF NOT %32
# | 7 | ASSIGN | x = (GCALL expanddims x)
# | 8 | ASSIGN | i = (GCALL add i 1)
# | 9 | GOTO | GOTO #29
# | 10 | LABEL | LABEL #30
# | 11 | ASSIGN | %ret = x
# | 12 | GOTO | GOTO RETURN
# | 13 | LABEL | LABEL RETURN
# | 14 | RETURN | RETURN %ret
#
# end
いい感じになってきましたね。ここまできたら簡易的なインタプリタを書いて実行することも簡単です。
今回の処理系でも Verify のために具体的な実行を担う
ConcreateInterpreter が実装されています。https://github.com/abap34/mu/blob/main/src/interpreter/concreateinterpreter.jl
型推論の実装
型遷移関数の実装
それでは、型推論を実装します。
そのためには抽象状態 (今回は上で出てきた型たち) とその順序 (今回は親子関係)、そして lowering された後の各命令について、抽象状態がどのように変化するかを表す意味関数を定義する必要があります。
上の型の集合を \( T \) , 命令全体の集合を \( I \) , 変数の集合を \( V \) とします。
抽象状態は、各変数の型ですから \( V \) から \( T \) への関数です。
そして、抽象状態上の順序関係を以下のように定めます。
\( A_1 \leq A_2 \Leftrightarrow \forall v \in V, A_1(v) \mathrel{<\colon} A_2(v) \)
ここで \( \mathrel{<\colon} \) は上で定義した親子関係です。
そして意味関数 \( ![.!]: I \to (V \to T) \to (V \to T) \) を以下のように定めます。
(実装は
1. InstrType が ASSIGN 以外のとき
抽象状態は変化しません.
2. InstrType が ASSIGN のとき
このとき抽象状態が変化します。
\( I_i \) が \( \text{var} \in V \) への代入だったとして、 \( ![I_i !] \) を考えることにしましょう。
InstrType が ASSIGN のとき、右辺は1. リテラルまたは変数のとき 2. builtin の呼び出し 3. generic function の呼び出し
の 3つで尽くされます。
1 のとき
単に右辺の値の型を調べてその変数の抽象状態を更新すればいいです。
つまり、抽象状態 \( a \) のときに定数 \( c \) の代入によって新たに得られる抽象状態 \( a' \) は
\[
a'(v) = \begin{cases}
\text{typeof(c)} &\quad v = \text{var} \\\\
a(v) &\quad \text{otherwise} \\\\
\end{cases}
\]
になります。(右辺が変数 \( b \) の場合は上の式で \( c \leftarrow a(b) \) です.
実装は
2 のとき
これも簡単で、builtin 関数は少ないのでその型遷移は書き下すことができます。 今回は
Julia言語も
Bool を返す、などは このハードコードされた型遷移関数を \( T_{\text{builtin}} \) と書くことにすると、 \( T_{\text{builtin}} \) は今回の設定ではビルトイン関数の名前と引数の型を受け取って帰り値の型 \( T \) を返すような関数です。
つまり \( \text{var} := f(t_{\text{arg}}) \) では
\[
a'(v) = \begin{cases}
T_{\text{builtin}}(f, t_{\text{arg}}) &\quad v = \text{var} \\\\
a(v) &\quad \text{otherwise} \\\\
\end{cases}
\]
となります。
3のとき
さて、問題は 3. の generic function の呼び出しです。
例えば推論のある段階で
x が Int または Float であることが判明しているとして、generic function f が Int に対する実装も Float に対する実装も持っている場合があります。このとき
f(x) はどちらのメソッドの呼び出しにもなりえますから、その返り値の集合から、安全であって最も具体的なもの、つまり最小上界を取れば良いです。 関数呼び出しの型遷移
generic function \( f \) を引数 \( t_{\text{arg}} \) で呼び出したときの型遷移関数 \( T_{\text{generic}} \) は、メソッドの型遷移を \( T_{\text{method}} \) , 呼び出しうるシグネチャと実装の組 \( (s, g) \) の集合を \( \mathcal{M} \) として
generic function \( f \) を引数 \( t_{\text{arg}} \) で呼び出したときの型遷移関数 \( T_{\text{generic}} \) は、メソッドの型遷移を \( T_{\text{method}} \) , 呼び出しうるシグネチャと実装の組 \( (s, g) \) の集合を \( \mathcal{M} \) として
\[
T_{\text{generic}}(f, t_{\text{arg}}) = \bigsqcup_{(s, g) \in \mathcal{M}} T_{\text{method}}(g, t_{\text{arg}} \sqcap s)
\]
ここで、 \( T_{\text{method}} \) の計算こそが求解アルゴリズムの仕事です。この中でも \( T_{\text{generic}} \) は使いますが、generic function \( f \) の呼び出しは最終的には builtin の呼び出しに到達しますから必ず計算可能です!
と言いたいところなのですが今回は実装の煩雑さ回避のために誤魔化しをしていて、うまくいかないケースがあります。末尾の 「この記事で誤魔化しているところ」を参照してください。
実装は
widening の実装
続いて widening を実装します。今回は次のような widening を実装することにします。
-
Union型の型パラメータが 10個を超えるまでは更新を続ける. - 10個を超えたら、型パラメータのうち共通の親であって最小の abstract type にする
今回は無限上昇鎖の構成は
Union 型を使ったもののみであること、abstract type が有限であることからこれは Widening Operator です。これを組み込んだ求解アルゴリズムを実装することで、型推論は常に停止します!
実装は
実行
ここまでを実装すれば、(多少インターフェースを整える必要はありますが、) 型推論が動くようになります!
試してみましょう。
次のようなとても単純な例で見てみます。
function f(){
if (true){
if (true){
return 1
} else {
return 1.0
}
} else {
return "hello"
}
}
}
この関数の返り値の型を推論してみると...
julia> ast = MuCore.parse(src); # パース
julia> lowerd = MuCore.lowering(ast); # lowering
julia> mt = MuBase.load_base(); # 標準ライブラリの入ったメソッドテーブルを用意
julia> MuCore.MuInterpreter.load!(mt, lowerd); # メソッドテーブルに src をロード
julia> MuTypeInf.return_type(lowerd[end], argtypes=[], mt=mt) # 推論!
mu.MuCore.MuTypes.Union{mu.MuCore.MuTypes.Union{mu.MuCore.MuTypes.Int, mu.MuCore.MuTypes.Float}, mu.MuCore.MuTypes.String}
🥳🥳🎉 見事! 返り値は
Int または Float または String と推論できています 🎉🥳🥳さらに、色々試せるよう、mu は mu自身で書かれた (とても貧弱で偏った) 標準ライブラリを備えています:
これを使って、widening の効果を実感してみましょう。
標準ライブラリを使うと以下のようなコードが書けます。
function expanddims(arr::AbstractArray){
result_size = append(size(arr), 1)
return reshape(arr, result_size)
}
function main(){
x = [1, 2, 3]
n = 100
i = 0
while (i < n){
x = expanddims(x)
i = i + 1
}
return x
}
expanddims は、配列の次元を増やすような操作です。 (もちろんこれはビルトインではなく、標準ライブラリの size や reshape などによって書かれた標準ライブラリの関数です。)この
main の返り値の型を推論してみます。julia> ast = MuCore.parse(src);
julia> lowerd = MuCore.lowering(ast);
julia> mt = MuBase.load_base();
julia> MuCore.MuInterpreter.load!(mt, lowerd);
julia> MuTypeInf.return_type(lowerd[end], argtypes=[], mt=mt)
mu.MuCore.MuTypes.AbstractArray
このように
AbstractArray と推論できています!これは widening による効果で、while 文の中で
Union{Array{Int, 1}, Array{Int, 2},Array{Int, 3}...} と更新され、これが 10回繰り返された時点で widening によって共通の親である AbstractArray になり、推論が収束しているわけです!ちなみに、どのような推論ができるかは
ディスパッチの静的解決
ここまで来ればこっちのもので、型推論によって各命令の実行直前の変数の型がいくらかわかりますから、マッチするメソッドが一つに限られるかを調べて、それによって置き換えれば良いです。
(すみません、これはタイトル詐欺で、この置換はまだ未実装です。ここまで来たら LLVM を使ってバイナリを吐けるようになる方が絶対面白いと思うので今後この部分は書きます。)
こうして高速な実行が可能になります。
この記事で誤魔化しているところ
Julia の処理系と比較すると当然大量の簡略化が入っているわけですが、主要な点を挙げると以下のようなものがあります.
- 型システムの簡略化 ─ ユーザ定義型をサポートしていませんしJulia の型システムはもう少し表現力豊かです。
- 相互再帰のサポート ─ 実は今回のアルゴリズムだけでは相互再帰で無限ループになるケースがあります。Julia 本体では相互再帰を含む関数呼び出しでも停止します。
- ビルトイン関数がちょっとリッチ ─ Julia のビルトイン関数はもう少し洗練されており、特に配列操作周りは今回は誤魔化してやや高レベルな操作が入っています。
- コンパイル時間の考慮がない ─ 全てを推論しています。
感想
やはり自分で実装することによって色々と明確になってよかったです。 次は SSA IR の最適化パートを読んでみようかと思います。
参考にした文献
- Bezanson, Jeffrey Werner. Abstraction in technical computing. Diss. Massachusetts Institute of Technology, 2015.
- Cortesi, Agostino. "Widening operators for abstract interpretation." 2008 Sixth IEEE International Conference on Software Engineering and Formal Methods. IEEE, 2008.
- https://github.com/aviatesk/grad-thesis
- https://github.com/JuliaLang/julia
[scitokyo] https://x.com/Ag_smith/status/1871469153233826192[jitcompile] Julia は関数が初見の型の組の引数で呼び出されたまさにそのときにコンパイルされるという意味で JIT コンパイル方式の言語と位置付けられていますが、 例えば V8 がするようなTracing による最適化は行いません。なので Julia は単にコンパイルのタイミングが遅かったりバイナリを明示的に名前がついたファイルとして出力しないだけで、実装の実態は AoT コンパイルに近いです。[arrayattent] (全ての要素が
T なわけではありません。例えば typeof(Real[1, 2.5, 3.5][1]) は Int です.)[bottom] Julia においては Union のパラメータは空とすることができます: Union{} . Julia においてはこの型は Core.TypeofBottom のエイリアスで、この記事でいうところの Bottom 型にあたります。[juliasubtyping] Zappa Nardelli, Francesco, et al. "Julia subtyping: a rational reconstruction." Proceedings of the ACM on Programming Languages 2.OOPSLA (2018): 1-27.[juliasubtypingdecide] Belyakova, Julia, et al. "Decidable Subtyping of Existential Types for Julia." Proceedings of the ACM on Programming Languages 8.PLDI (2024): 1091-1114.[jlsubtyping_undecidable] Belyakova, Julia, et al. "Decidable Subtyping of Existential Types for Julia." Proceedings of the ACM on Programming Languages 8.PLDI (2024): 1091-1114.[fastsubtyping] Chung, Benjamin, Francesco Zappa Nardelli, and Jan Vitek. "Julia's efficient algorithm for subtyping unions and covariant tuples (Pearl)." ECOOP 2019-33rd European Conference of Object-Oriented Programming. 2019.[setwidening] より一般に集合に対する演算として Widening Operator を定義する方法もあります。これは set-Widening Operator などと呼ばれます. 詳しくは Cortesi, 2008 などをみてください (参考文献にあります)